|
is based on Euclid's algorithm and determines the greatest common divisor of any given pair of positive integers. Find the time and space complexity of the RAM.
- The nonprimality problem defined by the following pair.
- Domain:
- { m | m is a natural number }.
- Question:
- Is the given instance m a nonprime number?
- The traveling-salesperson problem defined by the following pair.
- Domain:
- { (G, d, b) | G is a graph, d is a "distance" function that assigns a natural number to each edge of G, and b is a natural number }.
- Question:
- Does the given instance (G, d, b) have a cycle that contains all the nodes of G and is of length no greater than b?
- The partition problem defined by the following pair.
- Domain:
- { (a1, . . . , aN ) | N > 0 and a1, . . . , aN are natural numbers }.
- Question:
- Is there a subset S of {a1, . . . , aN } for the given instance (a1, . . . , aN ) such that (the sum of all the elements in S) = (the sum of all the elements in {a1, . . . , aN } - S)?
- The graph accessibility problem defined by the following pair.
- Domain:
- { (G, u, v) | G is a graph, and u and v are nodes of G }.
- Question:
- Is there a path from u to v in G for the given instance (G, u, v)?
- The c-bandwidth problem for graphs defined by the following pair, where c is a
natural number.
- Domain:
- { G | G is a graph }.
- Question:
- Does the given graph G = (V, E) have a linear ordering
on V with bandwidth c or less, that is, a one-to-one function
f: V
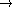 {1, . . . , |V |} such that |f(u)-f(v)|
{1, . . . , |V |} such that |f(u)-f(v)| 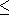 c for all (u, v)
in E?
c for all (u, v)
in E?
Hint: Use the following result.
Linear Speed-Up Theorem A T(n) time-bounded Turing machine M1 has an equivalent cT(n) time-bounded Turing machine M2 if T(n) > n and c > 0. Moreover, M2 is deterministic if M1 is so.
- Domain:
- { (a1, . . . , aN , b) | N
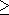 1, and a1, . . . , aN , b are natural
numbers }.
1, and a1, . . . , aN , b are natural
numbers }.
- Question:
- Are there natural numbers v1, . . . , vN such that a1v1 +


 +
aN vN = b for the given instance (a1, . . . , aN , b)?
+
aN vN = b for the given instance (a1, . . . , aN , b)?
for S2(n) = (S1(n))2 if the following two conditions hold.
- What is the bound that the proof implies for S2(n) if condition (1) is revised to have the form S1(n) < log n?
- Determine the time complexity of M2 in the proof of Theorem 5.5.2.
- Show that condition (2) can be removed.