[next] [prev] [prev-tail] [tail] [up]
-
7.1.1
- Let Q be the problem of determining the number of times the value 0 appears
in any given sequence. Describe a parallel program
 = <P, X, Y> of depth
complexity D(N) = O(log N) that solves Q. The parallel program should
allow each sequential program Pi to communicate with at most one other
sequential program Pj in each step.
= <P, X, Y> of depth
complexity D(N) = O(log N) that solves Q. The parallel program should
allow each sequential program Pi to communicate with at most one other
sequential program Pj in each step.
-
7.2.1
- Show that a CREW PRAM of linear size complexity and O(log n) depth
complexity, can output the sum of its input values.
-
7.2.2
- Show that a COMMON PRAM of linear size complexity, under the uniform
cost criterion, can determine in O(1) time whether an input consists only of
values that are equal to 1.
-
7.2.3
- Show that for each of the following statements there is a PRIORITY PRAM which
can, under the uniform cost criterion, determine in O(1) time whether the statement
holds.
- The number of distinct values in the input is greater than two.
- The input values can be sorted into a sequence of consecutive numbers
starting at 1.
-
7.2.4
- Show that one step of a PRIORITY PRAM can be simulated in constant depth
by a COMMON PRAM.
-
7.2.5
- A TOLERANT PRAM is a PRAM that resolves the write conflicts in favor
of no processor, that is, it leaves unchanged the content of the memory
cells being involved in the conflicts. Show that each TOLERANT PRAM
of size complexity Z(n) and depth complexity D(n) can be simulated by a
PRIORITY PRAM of size complexity Z(n) and depth complexity O(D(n)).
-
7.3.1
- Show that { x | x is in {0,1}*, and 1 appears exactly once in x } is decidable
by a family of circuits of size complexity O(n) and depth complexity
O(log n).
-
7.3.2
- Show that each circuit of size Z(n) and depth D(n) has an equivalent circuit,
of size at most Z2(n) and depth at most D(n)log Z(n), whose gates all have
outdegree of at most 2.
-
7.4.1
- Provide a table look-up circuit that accepts the language L = {1011, 0100,
1101, 1001}.
-
7.4.2
- Show that each of the following languages is decidable by a uniform family of
circuits of linear size complexity and O(log n) depth complexity.
- { 0i1i0i | i
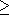 1 }.
1 }.
- { 0i1j | i
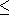 j }.
j }.
A gate g' is said to be the predecessor of a gate g in a circuit cn with respect to a path  if
any of the following cases holds.
if
any of the following cases holds.
-
 =
=  and g' = g.
and g' = g.
-
 is in {L, R}, and (g, t, gL, gR) is in cn for g
is in {L, R}, and (g, t, gL, gR) is in cn for g = g''.
= g''.
-
 =
=  1
1 2 for some g'' such that g'' is the predecessor of g in cn with respect
to
2 for some g'' such that g'' is the predecessor of g in cn with respect
to  1, and g' is the predecessor of g'' in cn with respect to
1, and g' is the predecessor of g'' in cn with respect to  2.
2.
The connection language LC for a family C = (c0, c1, c2, . . . ) of circuits is the language
{ (g, g',  ,
,  , n) |
, n) |  is in {L, R}*. |
is in {L, R}*. | |
| 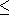 O(log (size of cn)). g' is the predecessor of g in
cn with respect to
O(log (size of cn)). g' is the predecessor of g in
cn with respect to  . If g' is a gate of type t in {¬,
. If g' is a gate of type t in {¬,  ,
,  } or a constant node t in {0, 1},
then
} or a constant node t in {0, 1},
then  = t, otherwise
= t, otherwise  =
= 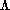 }.
}.
Example
Consider the circuit c2 of the following form.
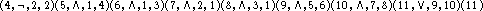
The gate g' = 9 of c2 is the predecessor of the gate g = 11 with respect to  = L, and
g' = 2 is the predecessor of g = 9 with respect to
= L, and
g' = 2 is the predecessor of g = 9 with respect to  = LRR (see Example 7.3.5 and
Figure 7.3.3).
= LRR (see Example 7.3.5 and
Figure 7.3.3).
For a family of circuits C that contains the circuit c2, both (11, 9, L,  , 2) and
(9, 2, LRR,
, 2) and
(9, 2, LRR, 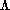 , 2) are in LC.
, 2) are in LC.
A family C = (c0, c1, c2, . . . ) of circuits is said to be uniformE if there exists a
deterministic Turing machine that accepts the language LC, and on any given input
(g, g',  ,
,  , n) the Turing machine halts in O(log ( size of cn)) time.
, n) the Turing machine halts in O(log ( size of cn)) time.
-
7.4.3
- Show that every uniformE family of circuits is also a uniform family of
circuits.
-
7.5.1
- Find SUBTAPE _MODIFIER for Example 7.5.1.
-
7.5.2
- Analyze the depth of cn in the proof of Lemma 7.5.1.
-
7.5.3
- Show that the containment U_DEPTH (D(n))
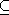 DSPACE (D(n)) holds for
fully space-constructible functions D(n).
DSPACE (D(n)) holds for
fully space-constructible functions D(n).
Hint: A circuit that recognizes a language has the following properties.
- The depth d of the circuit provides the upper bound of 2d on the size of
the circuit.
- Each node in the circuit can be represented by a path, given in reverse,
from the node in question to the output node.
-
7.5.4
- Show that U_NC1 contains NSPACE (1), that is, the class of regular
languages.
-
7.5.5
- Show that for each k
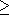 0 there are languages that are not in SIZE (nk).
0 there are languages that are not in SIZE (nk).
-
7.5.6
- Show that RP
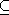
 k
k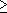 0SIZE (nk).
0SIZE (nk).
[next] [prev] [prev-tail] [front] [up]
![]() if
any of the following cases holds.
if
any of the following cases holds.
![]() = L, and
g' = 2 is the predecessor of g = 9 with respect to
= L, and
g' = 2 is the predecessor of g = 9 with respect to ![]() = LRR (see Example 7.3.5 and
Figure 7.3.3).
= LRR (see Example 7.3.5 and
Figure 7.3.3).
![]() , 2) and
(9, 2, LRR,
, 2) and
(9, 2, LRR, ![]() , 2) are in LC.
, 2) are in LC.![]()
![]() ,
, ![]() , n) the Turing machine halts in O(log ( size of cn)) time.
, n) the Turing machine halts in O(log ( size of cn)) time.