Find a probabilistic variation of the program that has O(n log n) expected time complexity.
Hint: A proof by induction can be used to show that T(n) = O(n log n) if
T(n) ![]() cn + 2/n
cn + 2/n ![]() i=0n-1 T(i).
i=0n-1 T(i).
- Step 1
- Randomly choose an entry (i, j) in matrix C for the given instance (A, B, C) of K, and let d1 denote the element at this entry.
- Step 2
- Use the ith row of A and the jth column of B to compute the value d2 at entry (i, j) of AB.
- Step 3
- Declare that the inequality AB
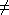 C holds if d1
C holds if d1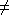 d2. Otherwise,
declare that AB = C.
d2. Otherwise,
declare that AB = C.
Hint: Note that a univariate polynomial s(x) of degree N has at most N roots, that is, N values x0 such that s(x0) = 0.
- Domain:
- { E(x1, . . . , xm) | E(x1, . . . , xm) is a polynomial expression with variables x1, . . . , xn }.
- Question:
- Does the given instance represent a Diophantine polynomial that is identically equal to zero?
- Show that if (v1, . . . , vm) is a nonzero vector of integers and d1, . . . , dm
are chosen randomly from {1, . . . , r} then d1v1 +


 + dmvm = 0 with
probability no greater than 1/r.
+ dmvm = 0 with
probability no greater than 1/r.
- Show that L = { a1bma2bm-1


 amb1 | m
amb1 | m 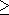 0 } is accepted by a
bounded-error probabilistic pushdown automaton.
0 } is accepted by a
bounded-error probabilistic pushdown automaton.
Hint: Use part (a) of the problem to check that the inputs have the form ai1bj1ai2bj2


 aimbjm with i2 - i1 - 1 = 0, i3 - i2 - 1 = 0, . . . and
j1 - j2 - 1 = 0, j2 - j3 - 1 = 0, . . .
aimbjm with i2 - i1 - 1 = 0, i3 - i2 - 1 = 0, . . . and
j1 - j2 - 1 = 0, j2 - j3 - 1 = 0, . . .
Hint: Allow M2 to halt in a rejecting configuration with probability (1/2)n and to start a new simulation of M1 with probability 1 - (1/2)n, after simulating a nonaccepting computation of M1.