|
Error Probability of Repeatedly Executed Probabilistic Programs
Outputs of Probabilistic Programs
For many practical reasons programs might be allowed a small probability of erring on some inputs.
Example 6.2.1 A brute-force algorithm for solving the nonprimality problem takes exponential time (see Example 5.1.3). The program in Figure 6.2.1 is an example of a probabilistic program that determines the nonprimality of numbers in polynomial expected time.
|
The program has zero probability for an error on inputs that are prime numbers.
However, for infinitely many nonprime numbers the program has a high probability of
giving a wrong answer. Specifically, the probability for an error on a nonprime
number m is 1 - s/(![]() - 1), where s is assumed to be the number of distinct
divisors of m in {2, . . . ,
- 1), where s is assumed to be the number of distinct
divisors of m in {2, . . . , ![]() }. In particular, the probability for an error reaches
the value of 1 - 1/(
}. In particular, the probability for an error reaches
the value of 1 - 1/(![]() - 1) for those numbers m that are a square of a prime
number.
- 1) for those numbers m that are a square of a prime
number.
The probability of getting a wrong answer for a given number m can be reduced by
executing the program k times. In such a case, the number m is declared to be nonprime
with full confidence, if in any of k executions the answer yes is obtained. Otherwise, m is
determined to be prime with probability of at most (1 - 1/(![]() - 1))k
for an error. With
k = c(
- 1))k
for an error. With
k = c(![]() - 1) this probability approaches the value of (1/
- 1) this probability approaches the value of (1/![]() )c
< 0.37c as m increases,
where
)c
< 0.37c as m increases,
where ![]() is the constant 2.71828 . . . However, such a value for k is forbidingly
high, because it is exponential in the length of the representation of m, that is, in
log m.
is the constant 2.71828 . . . However, such a value for k is forbidingly
high, because it is exponential in the length of the representation of m, that is, in
log m.
An improved probabilistic program can be obtained by using the following known result.
Result Let Wm(b) be a predicate that is true if and only if either of the following two conditions holds.
Then for each integer mThe result implies the probabilistic program in Figure 6.2.2.
|
The probability for a wrong answer can be reduced to any desired constant ![]() by
executing the program for k
by
executing the program for k ![]() log1/4
log1/4 ![]() times. That is, the number of times k that the
program has to be executed is independent of the input m.
times. That is, the number of times k that the
program has to be executed is independent of the input m.
Checking for the condition (bm-1 - 1) mod m![]() 0 can be done in polynomial time by
using the relation (a + b) mod m = ( (a mod m) + (b mod m) ) mod m and the relation
(ab) mod m = ((a mod m)(b mod m)) mod m. Checking for the condition gcd (bt - 1, m)
can be done in polynomial time by using Euclid's algorithm (see Exercise 5.1.1).
Consequently, the program in Figure 6.2.2 is of polynomial time complexity.
0 can be done in polynomial time by
using the relation (a + b) mod m = ( (a mod m) + (b mod m) ) mod m and the relation
(ab) mod m = ((a mod m)(b mod m)) mod m. Checking for the condition gcd (bt - 1, m)
can be done in polynomial time by using Euclid's algorithm (see Exercise 5.1.1).
Consequently, the program in Figure 6.2.2 is of polynomial time complexity. ![]()
Example 6.2.2
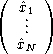
Consider the problem of deciding for any given matrices A, B, and C whether AB![]() C. A
brute-force algorithm to decide the problem can compute D = AB, and E = D - C, and
check whether
C. A
brute-force algorithm to decide the problem can compute D = AB, and E = D - C, and
check whether
| E |  |
The inequality AB![]() C holds if and only if the inequality
C holds if and only if the inequality
(AB - C)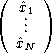 |
| | = | 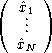 |
| | = | 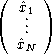 |
| | = | |||
| = | A | |||
| = | A | |||
| = | (AB - C) | |||
| = | 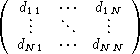  | |||
| = | 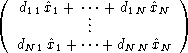 | |||
| | = | 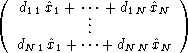 |
The analysis of the program for its error probability relies on the following result.
Result
Let d1x1 + ![]()
![]()
![]() + dN xN = 0 be a linear equation with coefficients that satisfy the
inequality (d1, . . . , dN )
+ dN xN = 0 be a linear equation with coefficients that satisfy the
inequality (d1, . . . , dN )![]() (0, . . . , 0). Then the linear equation has at most 2N-1
solutions (
(0, . . . , 0). Then the linear equation has at most 2N-1
solutions (![]() 1, . . . ,
1, . . . , ![]() N ) over {-1, 1}.
N ) over {-1, 1}.
Proof
Consider any linear equation d1x1 + ![]()
![]()
![]() + dN xN = 0. With no loss of generality
assume that d1 > 0.
+ dN xN = 0. With no loss of generality
assume that d1 > 0.
If (![]() 1, . . . ,
1, . . . , ![]() N ) is a solution to the linear equation over {-1, 1} then
(-
N ) is a solution to the linear equation over {-1, 1} then
(-![]() 1,
1, ![]() 2, . . . ,
2, . . . , ![]() N ) does not solve the equation. On the other hand, if both
(
N ) does not solve the equation. On the other hand, if both
(![]() 1, . . . ,
1, . . . , ![]() N ) and (
N ) and (![]() 1, . . . ,
1, . . . , ![]() N ) solve the equation over {-1, 1}, then the
inequality (-
N ) solve the equation over {-1, 1}, then the
inequality (-![]() 1,
1, ![]() 2, . . . ,
2, . . . , ![]() N )
N )![]() (-
(-![]() 1,
1, ![]() 2, . . . ,
2, . . . , ![]() N ) holds whenever
(
N ) holds whenever
(![]() 1, . . . ,
1, . . . , ![]() N )
N )![]() (
(![]() 1, . . . ,
1, . . . , ![]() N ).
N ).
As a result, each solution to the equation has an associated assignment that does
not solve the equation. That is, at most half of the possible assignments over
{-1, 1} to (x1, . . . , xN ) can serve as solutions to the equation. ![]()
Error Probability of Repeatedly Executed Probabilistic Programs
The probabilistic programs in the previous two examples exhibit the property of one-sided error probability. Specifically, their yes answers are always correct. On the other hand, their no answers might sometimes be correct and sometimes wrong. In general, however, probabilistic programs might err on more than one kind of an answer. In such a case, the answer can be arrived at by taking the majority of answers obtained in repeated computations on the given instance.
The following lemma analyzes the probability of error in repeated computations to establish an answer by absolute majority.
Lemma 6.2.1 Consider any probabilistic program P. Assume that P has probability e of providing an output that differs from y on input x. Then P has probability
of having at least N + 1 computations with outputs that differ from y in any sequence of 2N + 1 computations of P on input x.
Proof
Let P, x, y, and e be as in the statement of the lemma. Let ![]() (N, e, k) denote the
probability that, in a sequence of 2N + 1 computations on input x, P will have exactly k
computations with an output that is equal to y. Let
(N, e, k) denote the
probability that, in a sequence of 2N + 1 computations on input x, P will have exactly k
computations with an output that is equal to y. Let ![]() (N, e) denote the probability that, in a
sequence of 2N + 1 computations on input x, P will have at least N + 1 computations
with outputs that differ from y.
(N, e) denote the probability that, in a
sequence of 2N + 1 computations on input x, P will have at least N + 1 computations
with outputs that differ from y.
By definition,
The probability of having the answer y at and only at the i1st, . . . , ikth computations, in a sequence of 2N + 1 computations of P on input x, is equal to
i1, . . . , ik are assumed to satisfy 1 ![]() i1 < i2 <
i1 < i2 < ![]()
![]()
![]() < ik
< ik ![]() 2N + 1.
2N + 1.
Each collection {C1, . . . , C2N+1} of 2N + 1 computations of P has
possible arrangements Ci1 ![]()
![]()
![]() Cik of k computations. In these arrangements
only
Cik of k computations. In these arrangements
only
satisfy the condition i1 < ![]()
![]()
![]() < ik. Consequently, in each sequence of 2N + 1
computations of P there are
< ik. Consequently, in each sequence of 2N + 1
computations of P there are ![]() possible ways to obtain the output y for exactly k
times.
possible ways to obtain the output y for exactly k
times.
The result follows because ![]() (N, e, k) = (the number of possible sequences of 2N + 1
computations in which exactly k computations have the output y) times (the probability of
having a sequence of 2N + 1 computations with exactly k outputs of y).
(N, e, k) = (the number of possible sequences of 2N + 1
computations in which exactly k computations have the output y) times (the probability of
having a sequence of 2N + 1 computations with exactly k outputs of y). ![]()
In general, we are interested only in probabilistic programs which run in polynomial time, and which have error probability that can be reduced to a desired constant by executing the program for some polynomial number of times. The following theorem considers the usefulness of probabilistic programs that might err.
Theorem 6.2.1
Let ![]() (N, e) be as in the statement of Lemma 6.2.1. Then
(N, e) be as in the statement of Lemma 6.2.1. Then ![]() (N, e) has the following
properties.
(N, e) has the following
properties.
| 2 | = | 2 | ||
| = | ||||
| + | ||||
| = | ||||
| = | 1 |
implies the following inequality for 0 ![]() k
k ![]() 2N + 1.
2N + 1.
Consequently, the result is implied from the following relations that hold for
e = 1/2 - ![]() .
.
| = | ||||
| | (N + 1) | |||
| | (N + 1)22N+1eN+1(1 - e)N | |||
| = | (N + 1)22N+1 | |||
| = | 2 | |||
| = | 2e(N + 1)(1 - 4 | |||
| = | ||||
| = | ||||
| = | ||||
| > | ||||
| = | ||||
| = | ||||
| = | ||||
| = | ||||
| |
According to Theorem 6.2.1(a), a probabilistic program must have an error probability
e(x) smaller than 1/2, in order to reduce in the probability of obtaining a wrong solution
through repeatedly running the program. According to Theorem 6.2.1(b), error probability
e(x) smaller than some constant ![]() < 1/2 allows a reduction to a desired magnitude in
speed that is independent from the given input x. On the other hand, by Theorem 6.2.1(c)
the required speed of reduction is bounded below by f(x) = 1/( (1/2) - e(x) ), because
the probability
< 1/2 allows a reduction to a desired magnitude in
speed that is independent from the given input x. On the other hand, by Theorem 6.2.1(c)
the required speed of reduction is bounded below by f(x) = 1/( (1/2) - e(x) ), because
the probability ![]()
![]() of obtaining a wrong solution through repeatedly running
the program for f(x) times is greater than 1/(2
of obtaining a wrong solution through repeatedly running
the program for f(x) times is greater than 1/(2![]() 6). In particular, when f(x) is
more than a polynomial in |x|, then the required speed of reduction is similarly
greater.
6). In particular, when f(x) is
more than a polynomial in |x|, then the required speed of reduction is similarly
greater.
Outputs of Probabilistic Programs
The previous theorems motivate the following definitions.
A probabilistic program P is said to have an output y on input x, if the probability of P having a computation with output y on input x is greater than 1/2. If no such y exists, then the output of P on input x is undefined.
A probabilistic program P is said to compute a function f(x) if P on each input x has probability 1 - e(x) for an accepting computation with output f(x), where
e(x) is said to be the error probability of P. The error probability e(x) is said to be a bounded-error probability if there exists a constantBy the previous discussion it follows that the probabilistic programs, which have both polynomial time complexity and bounded-error probability, are "good" programs.