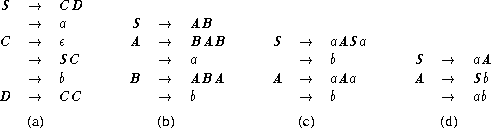- { (aibj, ajbi) | i, j
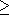 0 }
0 }
- { (x, aibj) | x is in {a, b}*, i = (number of a's in x), and j = (number of b's in x) }
- { (xyz, xyrevz) | xyz is in {a, b}* }
- { (aibj, ck) | i
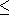 k
k 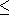 j }
j }
- { (aibj, ck) | k = min(i, j) }
- { (w, ck) | w is in {a, b}*, and k = min(number of a's in w, number of b's in w) }
- { (xy, yxrev) | x and y are in {a, b}* }
- { (x, xrevx) | x is in {a, b}* }
- { (x, y) | x and y are in {a, b}*, and y is a permutation of x }
|
- { vwwrev | v and w are in {a, b}*, and |w| > 0 }
- { x | x is in {a, b}* and each prefix of x has at least as many a's as b's }
- { aibjajbi | i, j > 0 }
- { w | w is in {a, b}*, and w
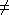 wrev }
wrev }
- { xxrev | x is accepted by the finite-state automaton of Figure 3.E.2 }
![[PICT]](theory-bk-three-3-E-2.jpg)
Figure 3.E.2
- { x | x = xrev and x is accepted by the finite-state automaton of Figure 3.E.2 }
|
|
![[PICT]](theory-bk-three-3-E-4.jpg)
|
Find a context-free grammar that generates L(M).
- { anblct | t > l > n > 0 }
- {

 rev
rev |
|  is in {a, b}* }
is in {a, b}* }
- {

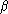
 rev
rev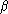 rev |
rev |  and
and 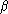 are in {a, b}* }
are in {a, b}* }
- { an
 an
an |
|  is in {a, b}*, and n = (the number of a's in
is in {a, b}*, and n = (the number of a's in  ) }
) }
- {
 #
#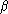 |
|  and
and 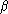 are in {a, b}* and
are in {a, b}* and 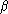 is a permutation of
is a permutation of  }
}
- {

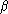 | The finite-state transducer whose transition diagram is given in
Figure 3.E.6
| The finite-state transducer whose transition diagram is given in
Figure 3.E.6
![[PICT]](theory-bk-three-3-E-6.jpg)
Figure 3.E.6
has output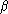 on input
on input  }
}
- { an! | n
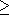 1 }
1 }
![[PICT]](theory-bk-three-3-E-7.jpg)
|